[pucha]

Конкурсная статья

PageRank

PageRank является запатентованным Google алгоритмом для расчета ссылочного веса веб страниц и обычно используется как синоним этого сочетания. Популярность PageRank объясняется простотой его вычисления - итеративная формула для расчета записывается одной строчкой:

Pr(A)[i] = 1 - d + d*(Pr(B1)[i-1]/C(B1) + ...+ Pr(Bj)[i-1]/C(Bj) + ... + Pr(Bk)(i-1)/C(Bk) , где (1)

Pr(A)[i] - PageRank для веб страницы A на i шаге расчета;
d - демпфирующий фактор, обычно принимается равным 0.85;
Bj - веб страницы, ссылающиеся на страницу A;
Pr(Bj)[i-1] - PageRank страниц, ссылающихся на A в момент расчета;
C(Bj) - число исходящих ссылок на странице Bj;

Итеративная процедура расчета PageRank для страниц сайта (сайтов) включает применение формулы 1 ко всем страницам рассматриваемого множества (сайт, сайты) в любой последовательности по одному разу для каждой страницы для одной итерации. Начальное значение PageRank для страницы не имеет большого значения (результат сходится к одной величине) и обычно принимается равным единице.

Если внимательно изучить формулу 1, то можно сделать следующие интересные выводы, применительно к замкнутому множеству страниц:

Выводы 1

1. PageRank страницы не может быть меньше 0.15.
2. Если страница не имеет исходящих ссылок на другие страницы сайта, то ее PageRank не участвует в дальнейших расчетах и мы получаем утечку общего PagePank сайта.
3. При отсутствии утечек каждая страница передает 0.85 своего PageRank другим страницам (ссылки сами на себя не рассматриваем).
4. Независимо от внутренней ссылочной структуры сайта, при отсутствии утечек, суммарный PageRank сайта равен числу его страниц.

Оптимальная топология сайта для сосредоточения веса на внутренней странице для ВЧ запроса

Критерием оптимальности топологии сайта для сосредоточения веса на K внутренних страницах сайта,
предназначенных для ВЧ запросов, выберем максимум отношения суммарного PageRank этих страниц к общему числу страниц сайта M, стремящемуся к бесконечности, при заданном ограничении на отношение отдельных PageRank между собой.

I = max(PR(1) + ... + PR(K))/M, при PR(1) = е2*PR(2) = e3*PR(3) =...=ek*PR(K), M -> ∞, где (2)

I - критерий оптимальности;
e2...ek - заданные пропорции между PageRank ВЧ страниц;
M - общее число страниц сайта;
PR(1)...PR(K) - PageRank ВЧ страниц;
Максимум ищется по всем возможным топологиям для сайта.

Правдоподобные утверждения для выбора оптимальной топологии

Рассмотрим следующие утверждения, вытекающие из Выводов 1

Утверждения 1

1. Максимум суммы PageRank ВЧ страниц при заданных ограничениях будет достигаться при минимуме суммарного PageRank остальных страниц сайта (во всяком случае верно для одной ВЧ страницы и для глобального максимума для нескольких ВЧ страниц).
2. Максимум PageRank ВЧ страницы сайта с одной ВЧ страницей не может больше чем половина общего PageRank сайта.
3. Глобальный максимум для суммы PageRank ВЧ страниц не может быть больше чем М - 0.15* (M - K), где М и К - общее число страниц сайта и число ВЧ страниц.

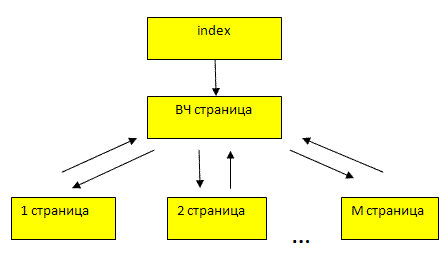
Из пункта 2 Утверждений 1 следует, что оптимальная топология для сайта с одной внутренней ВЧ станицей - это простая иерархия, отображенная на следующем рисунке.



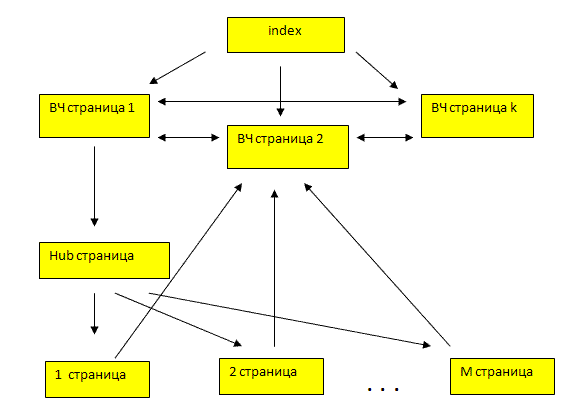
Для сайта с несколькими внутренними ВЧ страницами представляется перспективной топология со связанными между собой "сквозняком" ВЧ страницами и одной Hub страницей, представленная на следующем рисунке:




С ростом числа ВЧ страниц для этой топологии суммарный PageRank будет достаточно быстро стремиться к глобальному максимуму.

Проверка топологий на калькуляторе PageRank

Для проверки предложенных математических выкладок воспользуемся программой для расчета внутренних весов страниц сайта. Кроме предложенных топологий проверим еще два примера: топологию несвязанных между собой ВЧ страниц без Hub страниц и топологию связанных между собой ВЧ страниц без Hub страниц. Результаты расчетов приведены в следующей таблице. Общее число страниц M во всех эксперинтах равнялась 13.

Топология | Суммарный PageRank ВЧ страниц
Простая иерархия с одной ВЧ страницей - 6.05
Несколько связанных ВЧ и одна Hub страница - 9.77
Несколько связанных ВЧ без Hub страниц - 7.61
Несколько несвязанных ВЧ без Hub страниц - 6.21



Также можно загрузить лист excel с результатами расчета для всех приведенных топологий.


Как видно из приведенной таблицы теоретические выкладки хорошо подтверждаются результатами расчета.

[Cospi]

Ого, столько формул. Спасибо, сейчас по разбираюсь.

[webpavilion]

Cospi, формулам этим более 10 лет, у меня такое чувство что все статьи в рунете о пейджранге передираются с перевода Садовского статьи Криса Райдингсома. (http://digits.ru/articles/promotion/pagerank.html)

[terehoff]

Спасибнул, вспомнилась диссертация))), там у меня этих формул было...

[xitblogger]

вторая схема интересная, нужно будет попробовать